
L’apprentissage supervisé est une forme de machine learning, caractérisée par la création d’un algorithme qui apprend une fonction prédictive, en utilisant des données d’entrainement annotées. Dans l’article précédent, nous avions compris les bases de l’apprentissage supervisé ainsi que quelques applications.
Principaux algorithms de régression
Régression linéaire
La régression linéaire permet de prédire la valeur d'une variable dépendante (y) en fonction d'une ou plusieurs variables indépendantes données ( ,
,…). Cette technique de régression établit donc une relation entre x (l'entrée) et y (la sortie).
a. Régression linéaire simple
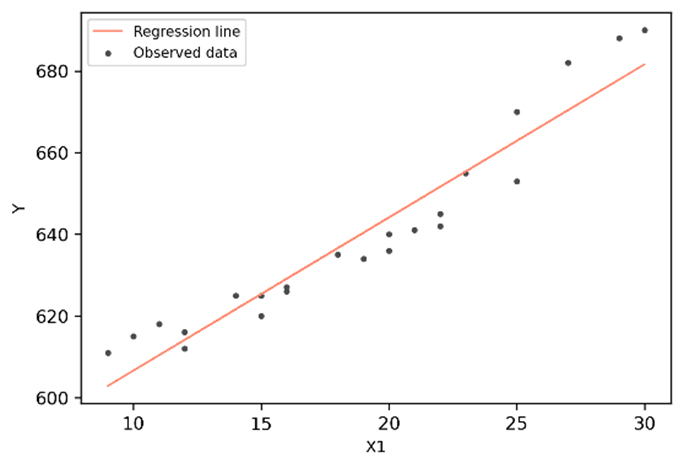
Ici, correspond à l'intersection 0 et
correspond au coefficient de x , soit la pente. Dans le cas d’un apprentissage supervisé, il est prévu que les valeurs de x et y soient données, lors de l’entrainement du modèle. Lors de ce processus, le modèle détermine la meilleure ligne droite, afin de prédire la valeur de y en fonction de la valeur de x donnée. Pour cela, le modèle doit identifier les meilleures valeurs pour
et
, tout en itérant à travers les données d’entrainement. Afin de déterminer les valeurs optimales pour
and
et évaluer la performance du modèle, nous pouvons utiliser des mesures d’évaluation. La plus répandue, pour mesurer la performance d’un modèle de régression, est la racine de l’erreur quadratique moyenne, ou REQM, qui correspond à la racine carrée de la moyenne des erreurs quadratiques. La formule est la suivante :
Dans cette formule :
- n est le nombre total de point de données
est la valeur de sortie réelle
est la valeur de sortie prédite
Une fois les valeurs optimales identifiées, le modèle devrait pouvoir établir une relation linéaire avec l’erreur minimale, soit la REQM minimale.
D’autres mesures d’évaluation, comme l’erreur quadratique moyenne (EQM), l’erreur moyenne en pourcentage absolu ou encore le coefficient de détermination () peuvent être utilisées.
La régression linéaire simple est le modèle le plus utilisé en finance. En effet, il peut être utilisé pour la gestion de portefeuille, l’évaluation des actifs et l’optimisation. Par exemple, il peut être employé pour prévoir les retours et les performances opérationnelles d’une entreprise. Cependant, il existe certains cas pour lesquels la variable à expliquer ne dépendent pas que d’un seul facteur. Ainsi, nous aurons besoin d’un modèle pour évaluer des situations un peu plus complexes : nous utiliserons la régression linéaire multiple.
b. Régression linéaire multiple
Dans certains cas, la variable de sortie (y), que nous essayons de prédire, dépend de plus d’une variable. Ainsi, un modèle plus élaboré, qui prend en compte cette dimension supérieure, est nécessaire. C’est ce qu’on appelle la régression linéaire multiple. L’utilisation d’un plus grand nombre de variables indépendantes peut permettre d’améliorer la précision du modèle, tant que les variables ajoutées sont pertinentes à celui-ci. Par exemple, un modèle de régression linéaire multiple basé sur trois variables indépendantes suivrait le format suivant :
De la même manière que pour la régression linéaire simple, des mesures d’évaluation peuvent être utilisées pour déterminer la performance optimale.
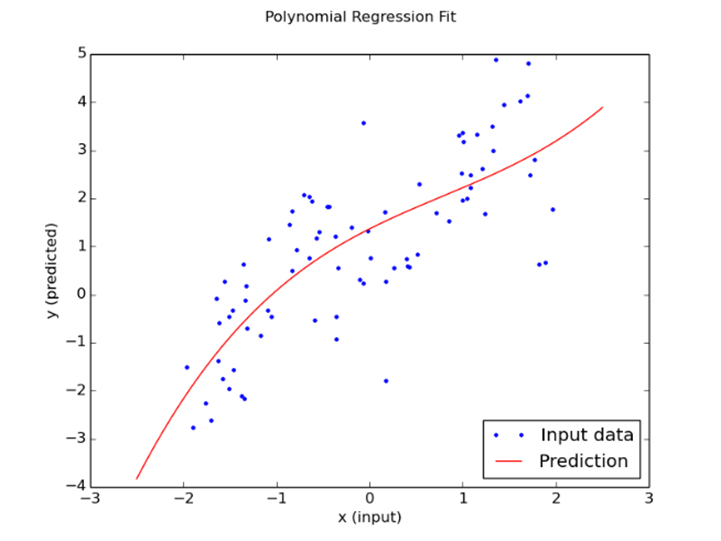
La régression polynomiale peut être considérée comme un cas particulier de la régression linéaire multiple, dans lequel la distribution des données est plus complexe qu’une simple distribution linéaire. En d’autres mots, la relation entre la variable dépendante x et la variable indépendante y est modélisée comme le N-ième degré polynomial de x. Cet algorithme peut générer une courbe pour des données non-linéaires. Par exemple, une régression linéaire polynomial peut suivre une fonction de la forme :
Un deuxième algorithme de régression est la régression de Poisson. C’est une forme particulière de régression, dans laquelle la variable à expliquer, y, doit être des données de dénombrement. En d’autres mots, cette variable doit correspondre à un chiffre supérieur ou égal à 0 and ne peut donc pas être négative. Avant de pouvoir appliquer une régression de Poisson, nous devons vérifier que les observations sont bel et bien indépendantes les unes des autres et que la distribution des données suit la distribution de Poisson.
Régression à vecteurs de support
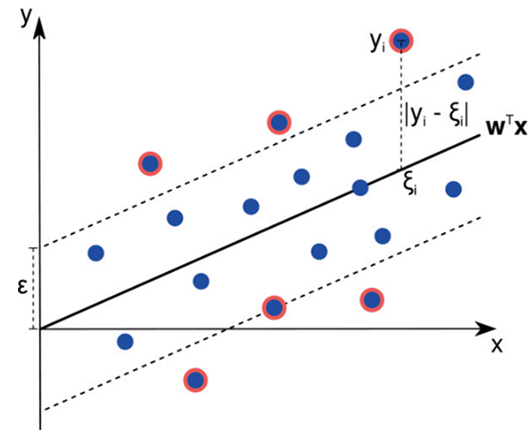
La régression à vecteurs de support, ou Support Vector Regression (SVR), est un algorithme de régression qui peut être appliqué aux régressions linéaires ainsi qu’aux régressions non-linéaires. Elle s’appuie sur le principe de machine à vecteur de support et est utilisée pour prévoir des variables continues ordonnées. Contrairement à la régression linéaire simple où le but est de minimiser le taux d’erreur, dans la régression à vecteur de support, l’idée est de faire rentrer l’erreur dans une marge prédéterminée et de maximiser l’écart entre les classes. En d’autres mots, cette forme de régression tente d’estimer la meilleure valeur au sein d’une marge, connue sous le nom de ε-tube.
A venir
Ainsi, il existe de nombreux algorithmes pouvant être utilisés pour la régression supervisée. Certains d’entre eux peuvent être également utilisés dans le cadre de problèmes de classification. Afin d’identifier quel algorithme de régression doit être utilisé, les utilisateurs doivent identifier le nombre de variables indépendantes présentes dans leurs données, ainsi que la relation entre les variables dépendantes et indépendantes.
Dans les prochains articles, nous nous concentrerons sur un cas d’usage d’apprentissage supervisé au sein de Linedata.
